Dancing Brunnian chains
In the course of a
project on
modelling Scottish Country Dances using braids, I posed the question
of how many dancers would be needed to dance along trajectories which,
when considered as braids, have a closure that is a Brunnian link.
Two families of Brunnian link, both of which are sometimes known as
"Brunnian rings" or "Brunnian rubberband links", were considered:
The "Bonio" has six crossings for each of the n components:
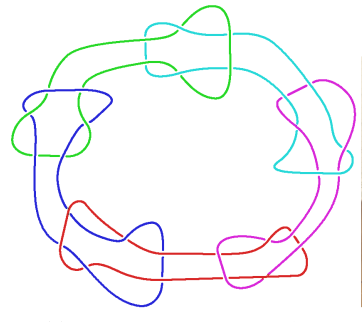
The "Horseshoe" has eight crossings for each of the n components:
The investigation into the question is written up in
a draft paper [PDF, 3MB]; it turns out
that (n+2) dancers are needed in both cases. Here, we show
constructions for the (n+2)-braids for both families (these
constructions are not unique).
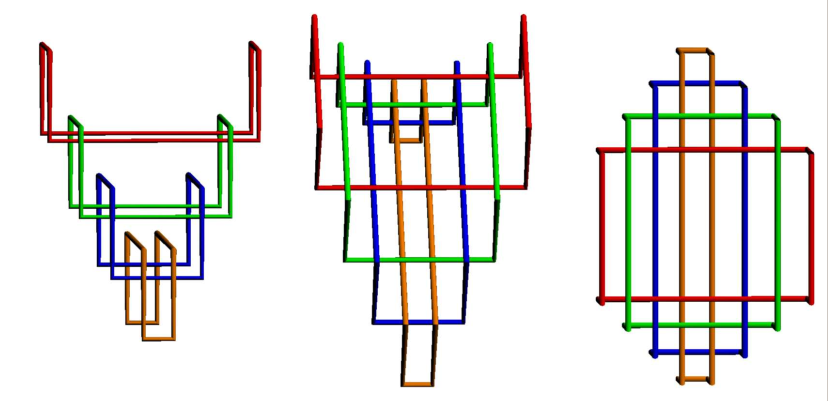
The Bonio
We pull (n-1) of the components of the link into a line, causing the
nth component to stretch out into a "connector" component, giving us a
"ladder" isotopy of the link:
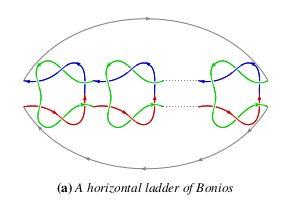
Next, we pull the overstrand end of each Bonio to the top of the
ladder (left) and the understrand end of each Bonio to bottom of the
ladder (right):
Finally, we flip the "connector" strands over to align the
orientations.
The images below show the "closed braid form" for the 1-Bonio, the
3-Bonio, and the 5-Bonio. These closed braids can be cut open anywhere
to provide a braid whose closure is the Bonio chain.
1-Bonio:
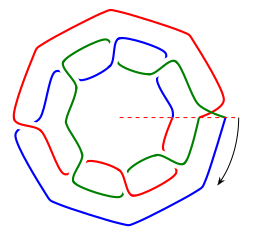
3-Bonio:
5-Bonio:
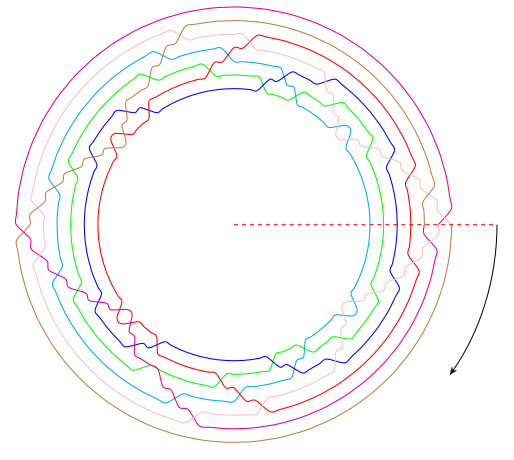
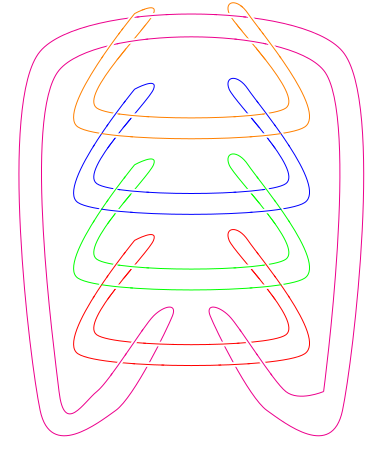
The Horseshoe
The key to finding the Horseshoe braid is to consider an alternative
projection of the link.
The transformation from the first version of the link to the
second is an isotopy, achieved by "flattening out" n-1 of
the link elements, causing the nth to stretch into a
"connector" element. The alternative projection in the third image
is perhaps less evident. The sequence below gives an idea, and the
embedded Asymptote
drawing can be used to manoeuvre the link manually to convince
yourself that these are indeed two projections of the same link
(the "connector" component is not shown in the Asymptote drawings).
Try it!
(click and drag)
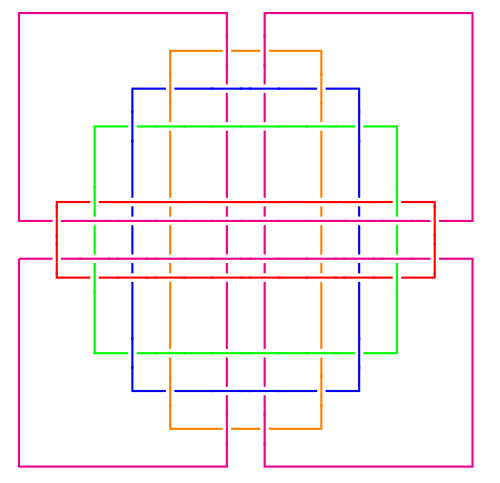
Transforming the new projection of the link
into closed braid form is simply a case of pushing the "connector"
strands running through the horizontal and vertical middle of the
square out to the edges. An interesting point, however, is that in so
doing, we "orient" this "connector" component in the opposite
direction to the others. The images below show the closed braid form
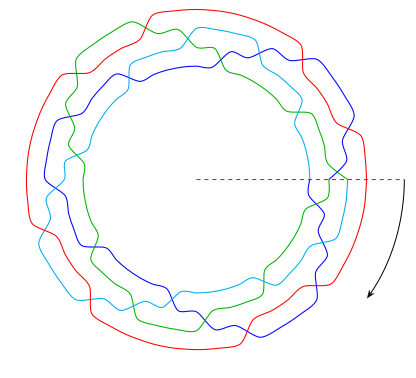
for the 2-, 4-, and 5-Horseshoe chains.
2-Horseshoe:
4-Horseshoe:
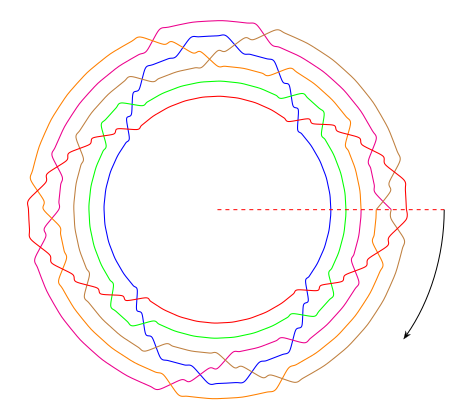
5-Horseshoe:
The toothy Horseshoe
The paper also looks briefly at variants of the links with extra
"teeth". Below (middle) is an Asymptote drawing of a "toothy" Horseshoe.
Try it!
(click and drag)
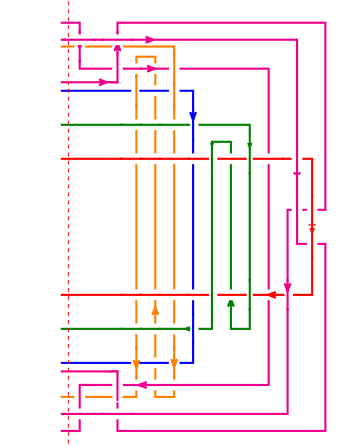
The "toothy" Horseshoe requires one extra
strand per extra tooth.
